Average Americans can assess mathematical arguments for beauty just as they can pieces of art or music, research finds.
The beauty they discerned about the math was not one-dimensional: Using nine criteria for beauty—such as elegance, intricacy, universality, etc.—300 people had better-than-chance agreement about the specific ways that four different mathematical proofs were beautiful.
This inquiry into the aesthetics of mathematics, published in Cognition, began when study coauthor and Yale University assistant professor of mathematics Stefan Steinerberger likened a proof he was teaching to a “really good Schubert sonata.”
“As it turns out, the Yale students who do math also do a statistically impressive amount of music,” says Steinerberger. “Three or four students came up to me afterwards and asked, ‘What did you mean by this?’ And I realized I had no idea what I meant, but it just sounded sort of right. So, I emailed the psych department.”
Psychology professor Woo-Kyoung Ahn replied to Steinerberger and, after further discussion, gave him the name of a psychology graduate student with whom she thought he would get along.
Enter Samuel G.B. Johnson, study coauthor and now assistant professor of marketing at the University of Bath School of Management, who was still completing his PhD in psychology at Yale when he connected with Steinerberger. Johnson studies reasoning and decision making. “A lot of my work is about how people evaluate different explanations and arguments for things,” he explains.
Steinerberger says Johnson understood immediately how to design an experiment to test his question of whether we share the same aesthetic sensibilities about math that we do about other modalities, i.e. art and music, and if this would hold true for an average person, not just a career mathematician like himself.
“I had some diffuse notion about this, but Sam immediately got it,” says Steinerberger. “It was a match made in heaven.”
Four proofs, four paintings, four sonatas
For the study, they chose four each of mathematical arguments, landscape paintings, and piano sonatas. Because the similarities between math and music have long been noted, Johnson explains, they also wanted to test people using another aesthetic modality—art in this case—to see if there’s something more universal about the way we judge aesthetics.
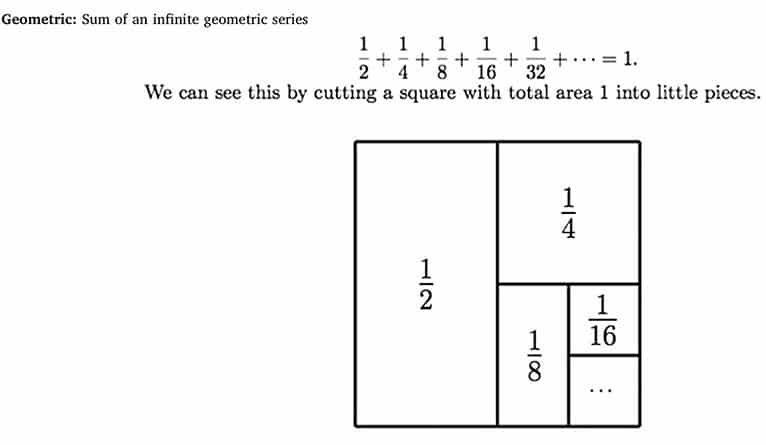
Johnson divided the study into three parts. The first task required a sample of individuals to match the four math proofs to the four landscape paintings based on how aesthetically similar they found them; the second required a different sample to do the same but instead comparing the proofs to sonatas; and the third required another unique sample of people to independently rate, on a scale of zero to ten, each of the four artworks and mathematical arguments along nine different criteria plus an overall score for beauty.
They derived these criteria from “A Mathematician’s Apology,” a 1940 essay by famous mathematician G.H. Hardy, which discusses mathematical beauty. The researchers’ nine dimensions elaborated from Hardy’s six were: seriousness, universality, profundity, novelty, clarity, simplicity, elegance, intricacy, and sophistication.
When Steinerberger and Johnson analyzed the ratings given by participants in part three, they found that for both the artworks and math arguments a high rating for elegance was most likely to predict a high rating for beauty.
The final step was to calculate the “similarity scores” for the participants in group three, which revealed how aesthetically similar they considered each proof and painting were to each other based on the separate beauty criteria. They then compared these scores to the results from the first group of participants, who were asked to simply match proofs with paintings based on their own intuitive sense of aesthetic similarity—much like Steinerberger’s initial analogy of the proof to a “good Schubert sonata.”
The beauty of math
When the results came in, Steinerberger and Johnson were surprised but pleased. They were able to take the similarity scores from participants in the third task to predict how the participants would behave in the first task. Participants in the third group agreed about which arguments were elegant and which paintings were elegant while, likewise, participants in the first group tended to match the argument the third group rated as most elegant with the painting they’d rated most elegant.
Laypeople not only had similar intuitions about the beauty of math as they did about the beauty of art but also had similar intuitions about beauty as each other. In other words, there was consensus about what makes something beautiful, regardless of modality.
“I’d like to see our study done again but with different pieces of music, different proofs, different artwork,” says Steinerberger. “We demonstrated this phenomenon, but we don’t know the limits of it. Where does it stop existing? Does it have to be classical music? Do the paintings have to be of the natural world, which is highly aesthetic?”
Math education
While quick to point out that they are not education scholars, both Steinerberger and Johnson see eventual implications of this research for math education, especially at the secondary school level.
“There might be opportunities to make the more abstract, more formal aspects of mathematics more accessible and more exciting to students at that age,” says Johnson, “And that might be useful in terms of encouraging more people to enter the field of mathematics.”
“I think if you understand what people consider beautiful in math, then it could give insight into how people understand math in the first place and how they process it,” adds Steinerberger. “There’s also the human implication of the question: How are we actually thinking about things as human beings? I think we have an obligation to collaborate with psychologists on this.”
For the study, the mathematical arguments they used were the sum of an infinite geometric series, Gauss’ summation trick for positive integers, the Pigeonhole principle, and a geometric proof of a Faulhaber formula.
The piano sonatas were Schubert’s “Moment Musical No. 4, D 780 (Op. 94)” [perf. David Fray]; Bach’s “Fugue from Toccata in E Minor (BWV 914)” [perf. Glenn Gould]; Beethoven’s “Diabelli Variations (Op. 120)” [perf. Grigory Sokolov]; and Shostakovich’s “Prelude in D-flat major (Op.87 No. 15)” [perf. Adrian Brendle].
The landscape paintings were Looking Down Yosemite Valley, California by Albert Bierstadt; A Storm in the Rocky Mountains, Mt. Rosalie by Albert Bierstadt; The Hay Wain by John Constable; and The Heart of the Andes by Frederic Edwin Church.
Source: Yale University



